4-DoF Robot - A Tutorial in MATLAB and Simulink
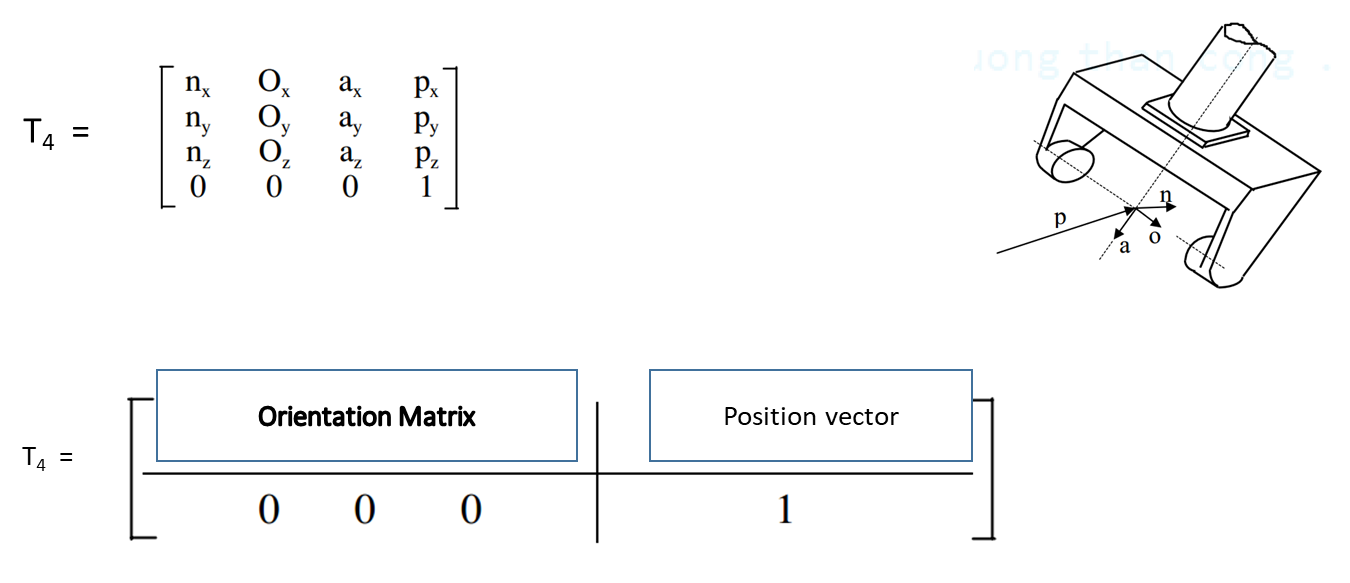
The forward kinematics problem is Calculating the matrix T4
Select the base coordinate system and attach the coordinate systems to the links.

Kinematic parameter (Denavit hartenberg)

Θi :Angle of rotation about the Z axis
α : Angle of rotation of the Z axis around the X axis (positive counterclockwise)
ai : Distance between axes Z
di: Distance between axes Z
General Matrix
An=Rot(z,θ)Trans(0,0,d)Trans(a,0,0)Rot(x,α)
cosθ -sinθcosα sinθsinα a cosθ
sinθ cosθcosα -cosθsinα a sinθ
An = 0 sinα cosα d
0 0 0 1
using MatLab to calculate the Matrix T4
T1 = [ C1 0 - S1 0;
S1 0 - C1 0;
0 -1 0 371;
0 0 0 1];
T2 = [ C2 - S2 0 505* C2;
S2 0 C2 505* S2;
0 0 1 0;
0 0 0 1];
T3 = [ C3 -S3 0 348*C3;
S3 C3 0 348*S3;
0 0 1 0;
0 0 0 1];
T4 = [ C4 -S4 0 109*C4;
S4 C4 0 109*S4;
0 0 1 0;
0 0 0 1];
T = T1*T2*T3*T4;
cos(θ1) =C1 ; cos(θ2) =C2 ; cos(θ3) =C3 ; cos(θ4) =C4 ;
sin(θ1) =S1 ; sin(θ2) =S2 ; sin(θ3) =S3 ; sin(θ4) =S4 ;
INVERSE KINEMATIC Is calculating θ1; θ2;θ3; θ4

tan(θ1 )= Py / Px =>
θ1 = atan2d(Py , Px)
Triangle O2O3O4:
O2O42= O2O32 +O3O42 -2O2O3*O3O4 cos(1800 –θ3 )
cos(1800 –θ3 ) =-cos(θ3 )= ((L2 )2 + (L3 )2 – O2O4 )/2*L2L3
Triangle O2CO4:
O2O42 =O2C2 + O4C2
C234 = cos(θ234)
S234 = sin(θ234)
Triangle O5EO4:
O4 E= L4 *Sin(θ234 )=L4*S234
O5E=L4 *Cos(θ234 )=L4*C234
O2C = O2 B – BC = √(〖Py〗^2+〖Px〗^2 ) - L4*C234
O4C = O4 E + EC = PZ - d1 + L4*S234
C3=cos(θ3)
C3 =[( √(〖Py〗^2+〖Px〗^2 ) - L4*C234 )2 + (Pz - d1 + L4*S234 )2 - (L22 + L32 ) ]/2*L2*L3 ;
S3=√(1-〖C3〗^2 )
θ3 = atan2d(S3 , C3)

Triangle O2 O4 K
Tan(α)=O4K/O2K
α= atan2(O4 K, O2K)
sin(θ3) = O4K/L3
cos(θ3) = O3K/L3
O4K = L3*S3
O2K = L2 + L3*C3
=> α = atan2(O4 K, O2K) = atan2(L3*S3, L2 + L3*C3 ) (1)
triangle O2 O4 C:
Tan(β)= O4C/O2C
β=atan2(O4C,O2C)
O2C = O2 B – BC = √(〖Py〗^2+〖Px〗^2 ) - L4*C234
O4C = O4 E + EC = PZ - d1 + L4*S234
θ2= α + β
θ4= θ234 – (θ2+ θ3)
https://drive.google.com/file/d/1hOsMSWyhtiUaL3Eh3_70ltjzmnmgTCBW/view?usp=sharing
https://www.youtube.com/watch?v=Jhte3nATu8k
Powered by Froala Editor
;